Astronomy 103
Measuring Angular Distances
Contents
- What is an angular distance?
- The small angle formula
- Why bother with angular distances?
- Using the crossbow
- Using the fist-and-finger rules
What is an angular distance?
When we talk about an angular distance, we are referring to two objects or two points that we can see. Consdier, for example, if you are looking at the bottom and the top of a 25'-high building that is 55' away from you:
![[Fig. 1]](angdistfig1.png)
The angle between the line of sight to the bottom of the building and the line of sight to the top of the building in this case is 24 degrees. (If you know a little trigonometry, you know how to figure that out.) We would then say that the angular distance from the bottom of the building to the top of the building is 24 degrees. Note that this is as measured by the person who is 55' away! (Would somebody who is closer measure a larger or a smaller angular distance?)
Another way to describe angular distance is the angle between your arms if you point your left arm at one object and your right arm at the other.
Sometimes we will talk about an angular size. This is the angular distance between the two ends of something. (It's just the same as the size of something being the physical distance between the two ends of something. Your height is the distance from your feet to the top of your head.)
The small angle formula
For small angles— a few degrees or less— there is a simple formula that relates the physical size, distance, and angular size:
In this case, h is the physical size of something, and d is the distance to that thing. (To use this formula, you must measure h and d in the same units. If you have h in meters and d in kilometers, you have to convert one of them before you use this formula.) Then a is the angle in radians. Because there are 360° in a circle, and there are 2π radians in a circle, you can figure out the angular size of something in degrees by adding a unit conversion to the formula:
Why bother with angular distances?
Since we know how to convert between angular and physical distances, why bother with angular distances at all? Consider what happens, however, if you don't know how far away something is. You see a rock. Is it a huge boulder that's far away, or is it a smaller rock that's closer to you? With a rock, you might be able to walk off the distance. However, with astronomy, it turns out that measuring distances to stars and galaxies can be very challenging. If you don't know the distance, then it's hard to figure out if you're looking at something that's bigger and farther, or if you're looking at something that's smaller and closer.
Angular distance, however, you can measure by staying in one spot (on the Earth, if you're talking astronomy). All you have to do is point from one side to the other side of an object, and measure the angle between the two directions of pointing. Or, if you want to look at the angular distance between two stars, first point at one, then point at the other, and measure the angle between the two directions of pointing.
Because stars can be at different distances away from us, two stars which are a relatively small angular distance apart may be physically farther from each other than two stars that have a large angular distance between them. For example, in the picture below, the physical distance between stars A and B is bigger than the physical distance between stars A and C, even though to the observer the angular distance is smaller.
![[Fig 2]](angdistfig2.png)
Using the Crossbow
![[Crossbow]](xbow1.jpg)
In the astronomy lab facility, we have angular distance measuring instruments known as crossbows (That is what they resemble, and indeed at least once campus security was called after people observed students with them at the edge of the parking garage.) The crossbow is basically a curved yardstick at the end of a straight wooden rod. If you place the base of the rod against your cheekbone and close the other eye, then you can line up two stars with measurements on the yardstick.
![[Crossbow]](xbow2.jpg)
The crossbows are designed so that two things which are measured to be 1" (one inch) apart on the yardstick if you have the base of the rod properly resting against your cheekbone, then those two things are exactly 2 degrees apart:
As an example of crossbow use, consider the picture below:
![[Crossbow Example]](xbow3.jpg)
Martha is measuring the distance between Betelgeuse and Bellatrix. Lining the crossbow up so that Betelgeuse is right over one of the inch marks, and rotating the crossbow so that Bellatrix is also right over the yardstick, they appear to her to be 3.5 inches apart. Thus, she has measured the angular distance between Betelgeuse and Bellatrix to be 7°.
In practice, when you're doing this in the dark, there won't be any light lighting up your hand, the crossbow, the yardstick, etc. To get around this, the yardsticks are painted with glow-in-the-dark paint. Hold the crossbow underneath a light (the waist-high lights outside the lab facility on the parking structure work well) for half a minute, and then use the crossbow while the paint is still glowing. To save your own night vision, avoid looking at the light yourself while you're holding the crossbow underneath it!
Also, in practice, there won't be giant glowing green letters in the sky telling you which star is which.
The crossbows are fragile and we have a limited number of them, so be careful with them. When you're done using one, return it to the equipment shed. If you leave them sitting or leaning about the lab facility, somebody else is liable to step on and break a crossbow. The many "half crossbows" in the equipment shed are a testament to this.
Using the Fist-and-Finger Rules
If you don't have a crossbow handy, it's still possible to measure angular distances. For most people, the ratio of the width of their hand to the length of their arm is nearly constant. As such, your hand spans a constant angular distance when you sight along a fully-extended arm.
There are several hand positions you can use: fist, fingers fully splayed, three fingers, one finger. Each of these measure a different angular distance. By using these and comparing how far apart stars appeared in comparison to your hand, you can gugue angular distances. It probably won't be as accurate or as precise as using the crossbow, but it will allow you to do naked-eye labs outside of the lab facility.
Hold your arm at full length, close one eye and sight along the arm with the other eye. Then, based on how you hold your hand, you can measure differnt angles:
| Hand Position | Nominal Angular Size |
Your Angular Size |
|---|---|---|
 |
1° | |
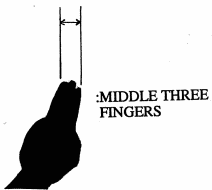
| 4° | |
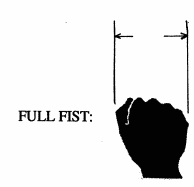 |
10° | |
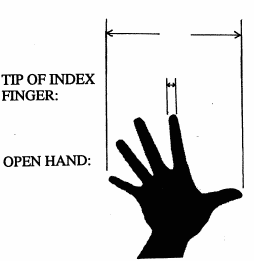 |
1.25° | |
| 18° |
Calibrate your hand!
While you can get reasonable results using the "nominal" values above, every's hand is a little bit different. Your little finger may not be as thick as mine, and only correspond to 1/2°, for example. To get better results, near the beginning of the semester, you should calibrate your hand using the crossbow, as illustrated by the following picture:

Here, Martha's fully open hand (thumb to little finger) spans 8.5" on the crossobow, which corresponds to 17°.
Do this for all of the positions on the table above, and enter the appropriate values for your hand in the "Your Angular Size" column on the table. Then use those values when employing the fist-and-finger method to measure angular distances outside of class.