Constructs of Symmetry in Islamic Art
by Terry Allen
Full Table of Contents
Section One. Types of Symmetry
Symmetry is a characteristic of nature; it
is not something that has been invented by
artists and architects. Symmetry
has been well investigated by mathematicians and crystallographers,
for example, and there is nothing for art historians to add to their
work; it can be used straightforwardly.
Symmetry comes in various forms no matter how it is analyzed.
Traditional Mathematical Approaches to Symmetry
A brief survey of
some of the literature that is understandable by
nonmathematicians, or at least was understandable by me, may serve
to introduce the mathematical view of symmetry.
I found that it was useful in understanding any particular point
to read several explanations of it.
Symmetry, by Hermann Weyl,
is much cited as a classic.1
Other mathematicians have followed him in tracing uses of symmetry in art
and in tracing occurrences of symmetry in nature and across mathematical
domains. His approach to actually explaining symmetry is progressive
rather than expository.
Transformation Geometry: An Introduction to
Symmetry,
by George E. Martin,
an undergraduate textbook,
provides a rigorous treatment of the relevant
topics;2
Connections: The Geometric Bridge between
Art and Science, by
Jay Kappraff,
is similarly rigorous but not quite as
formal.3
Tilings and Patterns, by
Branko Grünbaum and G.C. Shephard, is a broad and deep attempt
to establish a comprehensive mathematical description of tilings
and patterns (apparently not much dealt with previously from a mathematical
perspective), with ample
bibliography.4 It is avowedly written for students of mathematics and
professional mathematicians, conceding little to
“non-mathematicians whose interests include patterns and shapes
(such as artists, architects, crystallographers and
others),” the authors's protestations to the
contrary.5 Here I am concerned directly with neither
tilings nor patterns, but with symmetry;
I am sure there is much in Grünbaum and Shephard's book to be mined
by the humanist, but it will have to be mined by others. For those
interested in trying, I suggest focusing on those sections relating
to tilings and patterns that actually appear in art and
architecture, disregarding the general discussion of
possible patterns that no one has ever invented and impossible
(except for the geometrician) tilings composed of tiles that extend
infinitely in various directions. As for symmetry,
Grünbaum and Shephard discuss isometries in general and with
regard to tilings usefully.6
Symmetries of Culture: Theory and Practice of
Plane Pattern Analysis, by Dorothy K. Washburn and Donald W.
Crowe,
is a thoroughgoing handbook explaining how to analyze
two-dimensional patterns on archaeological and anthropological
artifacts in strictly mathematical
terms.7
Washburn and Crowe accessibly provide
historical and mathematical background as well as a methodology for
analysis (using flow charts, which is to say, proceeding
step by step through sets of questions that can be answered yes or
no).8
They point out that symmetry analysis (their term) of
repeating patterns was advocated
by anthropological archaeologists as early as the
nineteen-forties.
Wasmaʿa Chorbachi made a specific plea for the use of mathematical
terminology for symmetrical patterns in Islamic art in 1989 in
“In the Tower of Babel: Beyond Symmetry in
Islamic Design”,9 which also contains the most forthright remarks I have
seen in print regarding the corrosive effect on
the study of Islamic art
of large amounts of money flowing from the Muslim world to Western scholars
and institutions.
George Hersey, in
Architecture and Geometry
In the Age of the Baroque,
remarks “unfortunately, architectural historians and
critics almost never write about symmetry,”
and goes on to demonstrate simple forms of symmetry in sometimes
idiosyncratic interpretations.10
Certain basic concepts are presented simply in
an online article sponsored by the Math
Forum and the Textile
Museum, “Symmetry and Pattern:
The Art of Oriental Carpets”.
Symmetry can be a property of plane figures (such as regular
polygons); one-dimensional patterns, which are symmetrical in one
direction only (such as an undulating border pattern); and
two-dimensional patterns, which are symmetrical in more than one
direction (such as a checkerboard). These two-dimensional patterns
can be tiling patterns, in which one shape completely covers the
plane, or not.
There is an additional complication to two-dimensional
patterns, known as color symmetry, which I attempt to explain below.
I ignore three-dimensional symmetry here.
I am certain I have made errors in the following two sections,
but nothing ventured, nothing gained—I will be thankful to
readers who point them out to me.
Isometries
A plane figure or set of figures
can have multiple symmetries.
A symmetry in such a figure or figures is
the property of remaining
invariant through some transformation (that is,
and phrased informally, the distance between
any two points in the figure or set of figures
remains the same after the
transformation).11
Such a transformation
“leaves the figure looking exactly the same …
as it did
before”.12
There are four basic such transformations, which are known as
isometries (also discussed as
“motions”).13
Alternately,
symmetry is attributed to the motions rather than the figures
moved, from which point of view a symmetry of a figure or set of
figures is a motion that leaves the figure invariant. A special
case is the identity transformation: if a
figure is moved so that every point ends up in the same place as before
(for example, if a circle is rotated 360° through its center),
it is the same as it was before.
14
By contrast, stretching a figure along some axis, or enlarging
it, is a transformation but not an
isometry.15
The first transformation or motion
listed here, reflection, can, if repeated no more than
three times, produce the
effect of any of the other three,
but the results of a single application of each
of the four types differ.16
- reflection
A reflection takes place along an axis running
through the figure (or set of figures, or pattern).
A figure has reflection symmetry
if it is invariant after reflection (more colloquially, if it
appears the same after reflection). Neither
 nor
nor
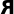 has reflection symmetry, but the
pair
has reflection symmetry, but the
pair

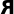
does. This pair
has a single axis along which it has reflection symmetry;
an equilateral triangle has three; a square
has four; a circle has
infinitely many;17
two circles next to each other have
one. Each of these symmetrical reflections counts as a symmetry,
so the figures listed have respectively one, three, four,
an infinite number, and one reflection symmetries.
- translation
Translation is the operation of moving a figure
in a single direction.
No single (or “finite”) figure has
translational symmetry, but an infinitely long and
evenly spaced row of identical figures
does: it can be moved by one or more multiples of the
distance between like points in the identical figures and remain the same.
As there are no such rows of figures in real life,
the mathematical concept of translation must be adapted to
finite rows of figures, such as colonnades or border patterns.
Here is an attempt to illustrate translation symmetry:
… 





 …
…
- rotation
Rotation in a plane is around a fixed point, the center of
rotation, whether that point is
part of the figure rotated or outside it.
Any regular
polygon (equilateral triangle, square, regular pentagon)
has rotational symmetry (around its center point).
So does a regular swastika. A regular polygon has
the same number of rotational symmetries as it has reflection
symmetries.18
Note that a figure can be rotated by any amount. Also, if the
center of rotation lies outside the figure, the result of the rotation
can result in a second figure lying at any angle to the original,
for example (and rather roughly):


See also the discussion below of rotocenters.
-
glide reflection
Glide reflection is “a translation (‘glide’)
followed by a reflection in a line parallel to the direction of
translation”19 or the same two transformations in reverse order,
like a line of footprints, the right footprints offset from the left
along the line of travel.
No single (“finite”) figure has
glide reflection symmetry (because it does not have translational
symmetry). Again, to adapt this notion to real life one must
be willing to consider rows of offset figures (footprints,
border patterns again) as qualifying:
… 



 …
…
…
… 



 …
…
These four types of isometry are simple enough to understand and
describe that there is really no reason to use any other terminology
for them, even in art historical studies. (Note, however, that
they do not suffice for describing tiling patterns, as the
the section “Field Patterns” in the Math Forum
article shows.)
Group Theory and Tilings
Group theory involves the concept of symmetry groups,
which are not difficult to understand given a grasp of isometries.
“Given any figure, the symmetry group
of that figure is the collection of all transformations that leave
that figure
invariant”;20
that is, the collection of all its symmetries.
Group theory, arising
from the consideration of symmetry groups, has achieved a quite
abstract level and is applied to all kinds of groups, not just
symmetry groups; I do not pretend that group theory is
relevant to art history. For the study
of tiling or “wallpaper” patterns
(in which a single repeated shape covers the entire plane), however,
it is of some interest
that any pattern that has translational symmetry has one of
only seventeen distinct symmetry groups (if one ignores
complications such as alternating colors).
Such patterns, which can be extended indefinitely in the imagination
(that is, they have unendliche
Rapport21)
are common in Islamic
art and architecture. (Also common are patterns that cover the
plane completely using more than one repeated shape, like the first
example from the Alhambra, below.)
Washburn and Crowe call these
“one-color, two-dimensional
patterns”. If the pattern has two colors that
are distributed regularly among its elements and a
transformation either moves all elements of one color
onto elements of the other (as with a
chessboard rotated 90°) or moves all elements onto like-color
elements,
it is a “two-color” pattern.22
As a side note, the translational symmetry of tiling
patterns can also
be analyzed in terms of “Dirichlet domains”. For a
point in a lattice of points that correspond along two axes, which need not
be at right angles as in the example below (nor need the points be
the same distance from each other in both axes)
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
a Dirichlet domain is “the entire region of
the plane that is nearer to that point than to any other lattice
point” (Devlin, op. cit., p. 163).
These regions (domains) likely cut across the actual units of design.
There are
only five distinct shapes of Dirichlet domain, all quadrilaterals or
hexagons. Generalizing this notion of lattices to three dimensions leads
fairly directly to crystallography, but is not, I believe, relevant
to the history of Islamic art, and for that matter, what
interests most art historians about tiling patterns is not the shape
of their Dirichlet domains but the shapes of the units composing the
pattern.
Notations for Patterns
There are multiple crystallographic notations for
patterns (plane symmetry groups), which I shall not
recapitulate here.23
Washburn and Crowe prefer a particular
commonly used set of notations that so far as I can see seems well
chosen, but for two-dimensional patterns these notations are
unfortuately cryptic
(even if one studies how they are constructed: each element
has a meaning)
and vulnerable to typographical error, such as
p2mg or
pb'gg.
But they are certainly preferable to
homegrown terminology such as the Math Forum article uses
(e.g., “rotations (2) + reflections + reflections”).
On the one hand it may be more important to know whether two
patterns share the same classification than to be able to give it a
memorable name; on the other, the characteristics of a pattern that
are captured in the structure of a
notation are disclosed by working with Washburn
and Crowe's flow charts, which are more interesting than they may
seem at first.
1. Ibid.
2. New York, 1982.
3. New York, 1991.
4. New York, 1987;
to be distinguished from
an abridged version published later under much the same title.
I have not seen the abridgement, and it may contain the material I
discuss here.
5. Ibid., p. vii.
For example,
“For any isometry σ and any set
S
we write σS for the image of
S under σ.”
6. Ibid.,
pp. 26–45.
7. Seattle, 1988. See also Clare E.
Horne,
Geometric symmetry in
patterns and tilings,
Cambridge, 2000.
8. This is not to say that using the
flow charts is particularly easy; one must
work back and forth through the text (which is not rigidly
consistent in its terminology) to understand just what the
questions mean. Studying their examples can help, although studying
the rules governing their notation may not.
9. Unfortunately
buried from view by art historians in
Symmetry 2: Unifying Human Understanding,
ed. István Hargittai, Oxford, 1989, pp. 751–89.
10. Chicago,
2000, p. 99.
11. For a formal
definition see Martin, op. cit., p. 26: for the geometrician, a
transformation of a figure produces a new set of points; the
distance that remains the same is then between points in the
original figure and the corresponding points in the figure after
transformation.
12. Keith Devlin,
Mathematics: The Science of Patterns,
New York, 1994, repr. 2003, p. 146.
13.
See Washburn and Crowe, op. cit., pp. 44ff.,
which I find slightly difficult;
their way of describing these transformations, also used by Weyl, is that
a plane figure is symmetric with respect to a given line
if it is “carried into itself” by reflection in that
line (as opposed to changing it into a different figure; Weyl,
op. cit., p. 43). They also write of “motions of the
plane”. Martin, op. cit., p. 18, points out that no motion is
actually involved; “transformations are just one-to-one
correspondences among the points” of figures. One need
not worry about how to manipulate a plane of infinite extent.
14. Kappraff, op. cit., p. 390,
and
Grünbaum and Shephard, op. cit., p. 26, seem to
treat it as a
distinct isometry, but it is often ignored as a type
as uninteresting except
for set theory.
15. Martin, op. cit., p. 1.
16. Martin, op. cit.,
ch. 5.
17. See Weyl, op. cit., p.
46 for the circle.
18. Counting
a 360° rotation around its center, which is
the identity isometry; Grünbaum and Shephard, op. cit., p.
27, fig. 1.3.2.
19. Washburn and Crowe,
op. cit., p. 50.
20. Devlin, op. cit.,
p. 146.
21. See Terry Allen,
Five Essays on Islamic Art,
Sebastopol, Calif., 1988,
chapter 1.
22. Op. cit.,
p. 57, 63ff. Washburn and Crowe discuss briefly but do not
consider in detail patterns involving three and more colors.
23. See Chorbachi,
op. cit., 774–75, who does not express a preference
except for uniformity in use of one notation or another.
 nor
nor
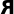 has reflection symmetry, but the
pair
has reflection symmetry, but the
pair






…




… …




…
